Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationValidation CasesValidation Case: Turbulent Pipe Flow

    Validation Case: Turbulent Pipe Flow

    This turbulent pipe flow validation case belongs to fluid dynamics. The aim of this test case is to validate the following parameters:

    • Pressure drop between the inlet and outlet of the pipe
    • Velocity distribution across the flow direction

    The simulation results of SimScale were compared to a reference solution based on the Power law velocity profile presented by Henryk Kudela in one of his lectures\(^1\).

    View Project

    Geometry

    The geometry can be seen below:

    pipe geometry turbulence and pressure drop validation
    Figure 1: The geometry of the pipe to study turbulent flow and pressure drop

    This is a cylindrical pipe with a diameter of 0.01 \(m\), and a length of 1 \(m\).

    Analysis Type and Mesh

    Tool Type: OpenFOAM®

    Analysis Type: Incompressible steady-state analysis.

    Turblence Model: Two turbulence models were tested, the k-epsilon and the k-omega SST.

    Mesh and Element Types:

    Two approaches were tested in this validation case: Wall functions and full resolution on the walls. For the wall functions, the desired \(y^+\) range is [30 , 300], and the generated mesh looks like this:

    wall treatment with wall functions for boundary layer of mesh
    Figure 2: The mesh created for the wall function approach

    Full resolution on the walls requires a \(y^+\) lower than \(1\), so the final mesh has the following form:

    wall treatment with full resolution for boundary layer of mesh
    Figure 3: The mesh created for the full resolution approach with inflation layers added

    More details about the meshes used in the three cases can be seen bellow:

    CasesNear-wall approachNumber of cellsMesh typeTurbulence model
    AWall functions176574Standardk-omega SST
    BWall functions176574Standardk-epsilon
    CFull resolution1393776Standardk-omega SST
    Table 1: Information on the meshes used for each case

    Simulation Setup

    Fluid:

    • Water
      • \((\nu)\) Kinematic viscosity = 10\(^{-6}\) \(m^2 \over \ s\)
      • \((\rho)\) Density = 1000 \(kg \over\ m^3\)

    Boundary Conditions:

    • Velocity inlet of 1 \(m \over \ s\)
    • Pressure outlet of 0 \(Pa\)
    • No-slip walls with wall functions for cases A and B, and full resolution for case C

    Initial Conditions:

    • Turbulent kinetic energy \((k)\) of 3.84e-3 \(m^2 \over \ s^2\)
    • Case A & C: Specific dissipation rate (\(ω\)) of 88.53 \(1 \over \ s\)
    • Case B: Dissipation rate \((ε)\) of 3.059e-2 \(m^2 \over \ s^3\)

    Reference Solution

    The velocity profile for turbulent pipe flow is approximated by the Power-law velocity profile equation \(^1\):

    $$\bar{u}_y(r) = \bar{u}_{y_{max}}\left(\frac{R-r}{R}\right)^{1/n}$$

    where:

    • \({u}_{y_{max}}\): the maximum y-velocity of the cross-section (along the pipe axis)
    • \(R\): the radius of the cylinder
    • \(r\): the distance from the center of the cross-section
    • \(n\): a constant that depends on the Reynolds number, estimated as 7 for this case

    For turbulent flow, the ratio of \(u_{y_{max}}\) to the mean flow velocity is a function of \(Re\). In this case, this ratio is calculated to be 1.224.

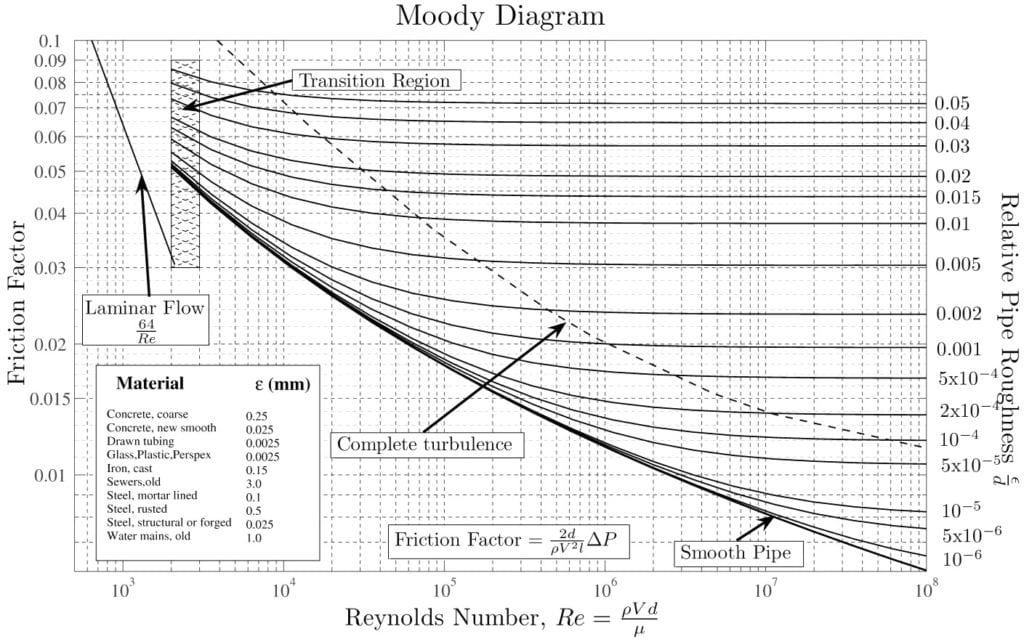
    The pressure drop for turbulent flow in pipes is obtained by using the Darcy-Weisbach \(^2\):

    $$\Delta P = f\ \frac{\rho\ u^2 \ l}{2 \ d}$$

    where:

    • \(f\): is the Darcy friction factor calculated by the solution of the Colebrook equation
    • \(ρ\): is the density of the fluid
    • \(u\): is the average velocity of the cross section
    • \(l\): is the length of the pipe
    • \(d\): is the diameter of the cylinder

    According to the Moody diagram (Figure 4) and for this case, the value of \(f\) is 0.0309.

    moody diagram for pipe flow analytical solution
    Figure 4. Moody diagram for estimating the Darcy friction factor

    Result Comparison

    Wall functions

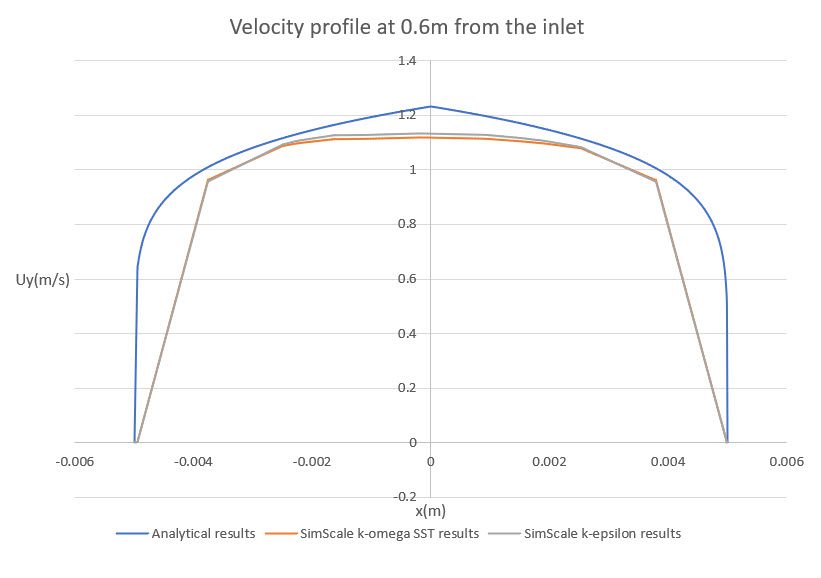
    For the “wall function approach” the average \(y^+\) value on the walls of the pipe is 31.95 for k-omega SST and 32.39 for k-epsilon.

    Pressure drop along the pipe length can be observed below:

    comparison of pressure drop across the pipe for turbulent flow with wall functions k-epsilon and k-omega SST model
    Figure 5: The pressure drop across the pipe with the wall functions approach

    The following graph shows the developed velocity profile, located 60 \(cm\) from the inlet:

    comparison of velocity profiles across the x direction for turbulent pipe flow with wall functions k-epsilon and k-omega SST model
    Figure 6: The velocity profile across the x axis, on a plane located 0.6 \(m\) from the inlet with the wall functions approach

    Full resolution

    For “full resolution”, the average value for \(y^+\) is 0.017. The corresponding graphs are created:

    The pressure drop along the pipe length:

    comparison of pressure drop across the pipe for turbulent flow with full resolution and k-omega SST model
    Figure 7: The pressure drop across the pipe with the full resolution approach

    The developed radial velocity profile, located 60 \(cm\) from the inlet:

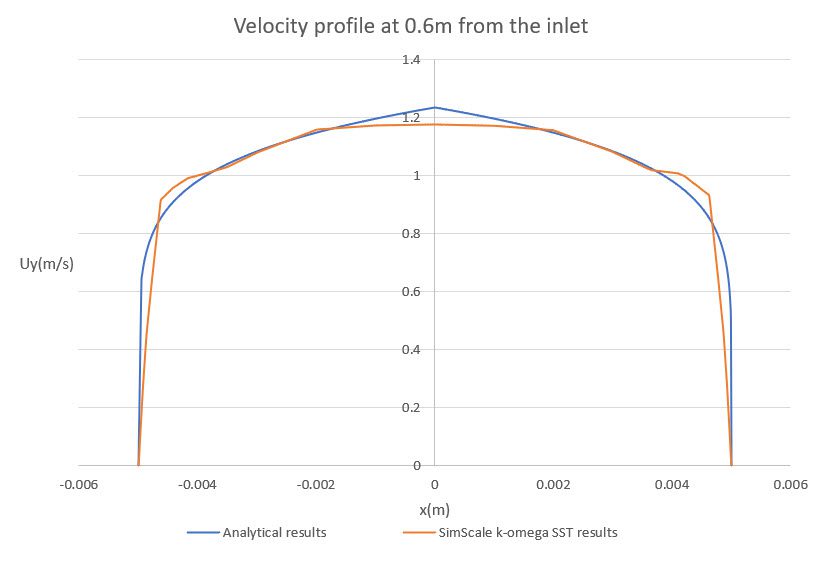
    comparison of velocity profiles across the x direction for turbulent pipe flow with full resolution and k-omega SST model
    Figure 8: The velocity profile across the x-axis, on a plane located 0.6 (m) from the inlet with the full resolution approach

    Besides good agreement with the Power law model, results show that all approaches and turbulence models are successful in predicting the pressure drop along pipe length for the given meshes.

    pressure distribution on pipe turbulent flow
    Figure 9: Pressure distribution across the pipe for Case A

    References

    Note

    If you still encounter problems validating you simulation, then please post the issue on our forum or contact us.

    Last updated: July 5th, 2023

    Contents