Validation Case: Thermal Stress Analysis of Polymeric Photo-Thermal Microactuator

This thermal stress analysis of a polymeric photo-thermal microactuator validation case belongs to thermomechanics. This test case aims to validate the following:

• Thermomechanical solvers

The simulation results of SimScale were compared to the analytical results presented in [Elbuken et al.]\(^1\).

Geometry

A total of 13 microactuator geometries are evaluated in this validation case. The base geometry is shown below:

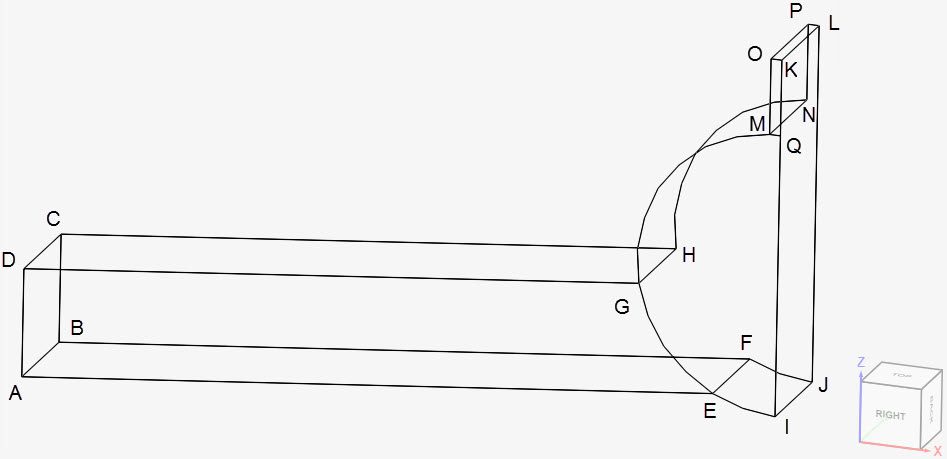
The 13 geometries are divided into two groups. Using Figure 2 as a reference, for the group A geometries, the length L and width W of the microactuator remains constant, whereas the bending angle \(\theta\) varies.

For group B, the length L and bending angle \(\theta\) are constant, and the width W changes. For all geometries, the radius R and thickness of the microactuator, in the y-direction, remains constant. Due to symmetry, only half of the model was taken for the analysis.

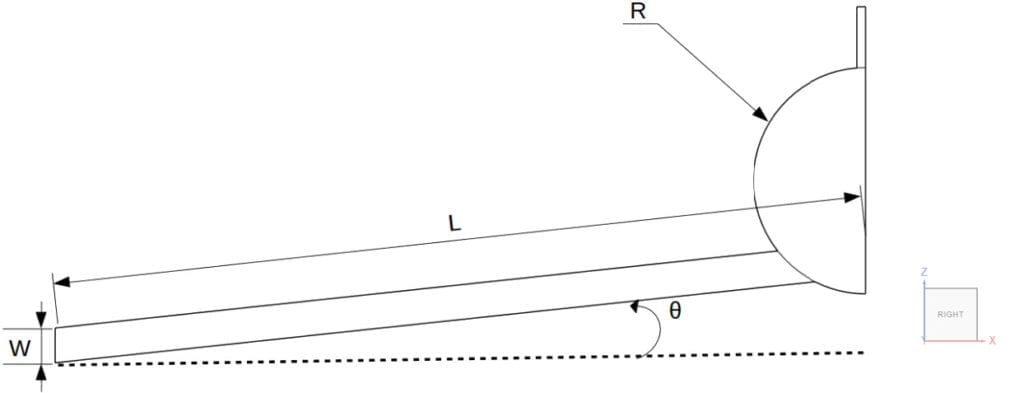
Table 1 provides an overview of the dimensions:

Case	R \([\mu m]\)	Thickness in y-direction \([\mu m]\)	W \([\mu m]\)	L \([\mu m]\)	\(\theta\) [º]
A1	130	100	50	1000	6
A2	130	100	50	1000	8
A3	130	100	50	1000	10
A4	130	100	50	1000	12
A5	130	100	50	1000	14
B1	130	100	30	700	6
B2	130	100	40	700	6
B3	130	100	50	700	6
B4	130	100	60	700	6
B5	130	100	70	700	6
B6	130	100	80	700	6
B7	130	100	90	700	6
B8	130	100	100	700	6

Analysis Type and Mesh

Tool Type: Code Aster

Analysis Type: Thermomechanical analysis type

Mesh and Element Types: All meshes were created with the standard algorithm, using second-order elements. Table 2 presents a summary of the meshes:

Case	Mesh Type	Nodes	Element Type
A1	2nd-order standard	194853	Standard
A2	2nd-order standard	479747	Standard
A3	2nd-order standard	360734	Standard
A4	2nd-order standard	466753	Standard
A5	2nd-order standard	257295	Standard
B1	2nd-order standard	102941	Standard
B2	2nd-order standard	134074	Standard
B3	2nd-order standard	130987	Standard
B4	2nd-order standard	132192	Standard
B5	2nd-order standard	142016	Standard
B6	2nd-order standard	152533	Standard
B7	2nd-order standard	165596	Standard
B8	2nd-order standard	173364	Standard

Find below the mesh used for case B8. It’s a standard mesh with second-order tetrahedral cells.

Simulation Setup

Material:

• Custom material – SU-8
  • Material behavior: linear elastic
  • \(E\) = 4 \(GPa\)
  • \(\nu\) = 0.22
  • \(\rho\) = 1200 \(kg/m³\)
  • \(\kappa\) = 0.2 \(\frac {W}{m.K}\)
  • Expansion coefficient = 5.2e-5 \(1/K\)
  • \(T_0\) Reference temperature = 300 \(K\)
  • Specific heat = 1500 \(\frac {J}{kg.K}\)

Boundary Conditions:

• Constraints
  • Fixed support on face ABCD;
  • \(d_x\) = 0 on face JIQKL.
• Temperature loads
  • Fixed temperature value of 300 \(K\) on face ABCD.
• Heat flux loads
  • Surface heat flux boundary condition of 9433.96 \(W/m²\) face IEGMQ.
  • Convective heat flux boundary condition on all faces, except ABCD and JIQKL. The heat transfer coefficient is 10 \(\frac {W}{K.m^2}\) and the \(T_0\) reference temperature is 300 \(K\).

Reference Solution

The analytical solution is given by the equations presented in [Elbuken et al.]\(^1\).

Result Comparison

Find below the comparison between the analytical solution and SimScale results. The quantity measured is the displacement of the tip of the structure (face OPLK).

The first plot shows the results for cases A1 through A5:

Similarly, for cases B1 through B8, Figure 5 shows the result comparison:

In Figure 6, we can see the displacement contours for case B8:

Last updated: November 7th, 2023