Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationValidation CasesValidation Case: Fixed Beam Under Changing Temperature

    Validation Case: Fixed Beam Under Changing Temperature

    This validation case belongs to solid mechanics. The aim of this test case is to validate the following parameters on a fixed beam, that is subjected to a temperature change of 10 \(K\):

    • Unit stress \((\sigma)\)

    The simulation results of SimScale were compared to the results presented in [Roark]\(^1\).

    View Project

    Geometry: Fixed Beam

    A bar with a square cross-section was used for this case:

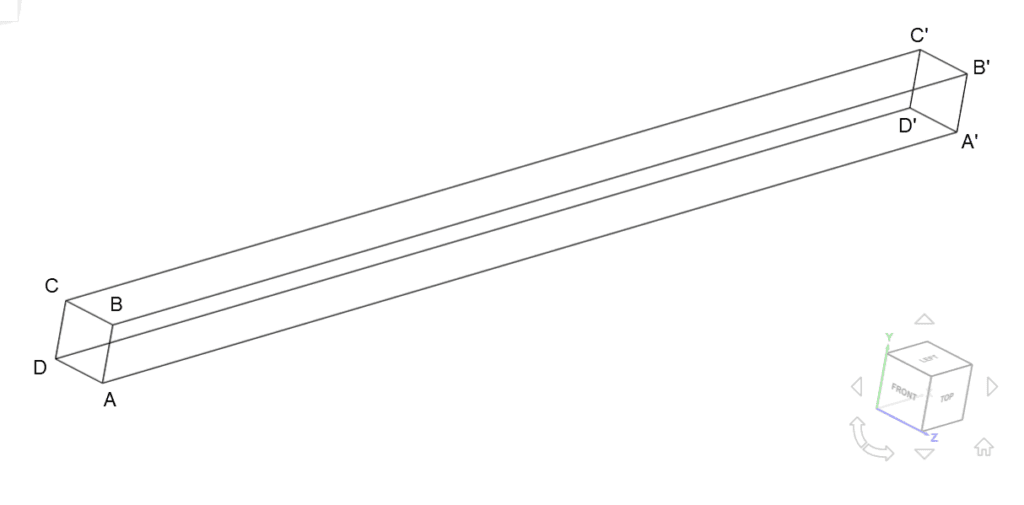
    fixed beam used for the validation case
    Figure 1: The fixed rectangular beam geometry with square cross-section

    The cross section area of the bar is \(A\) = 0.05 x 0.05 \(m^2\) and it’s length is \(l\) = 1.0 \(m\).

    Analysis Type and Mesh

    Tool Type: Code_Aster

    Analysis Type: Thermomechanical, linear with static inertia effect

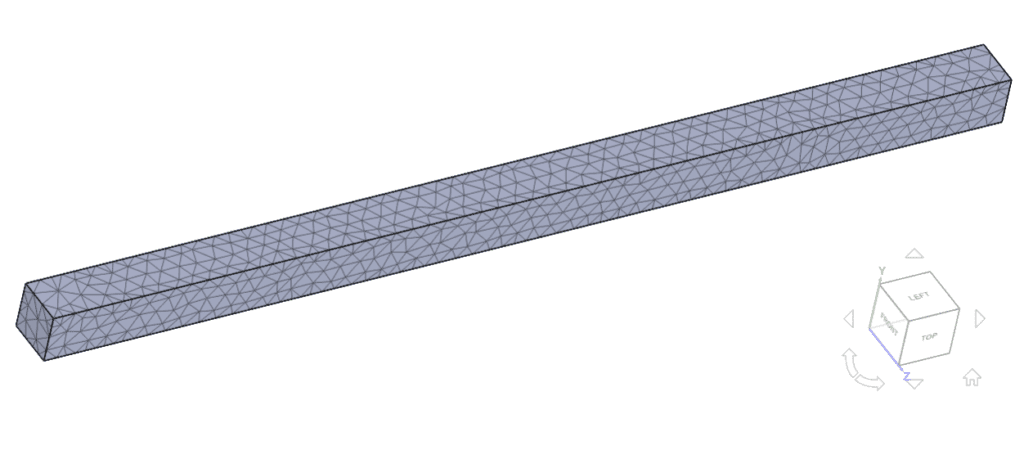
    Mesh and Element Types:

    The meshes used in (A) and (B) were created with the Standard mesher tool on the SimScale platform. Details can be found in Table 1:

    CaseMesh typeNumber of nodesElement type
    AStandard14841st order tetrahedral
    BStandard93202nd order tetrahedral
    Table 1: The details of each mesh that was simulated within the validation project
    linear tetrahedral mesh created with the standard mesher
    Figure 2: The 1st order mesh for case A, created with the Standard mesher algorithm in SimScale

    Simulation Setup

    Material:

    • Steel (linear elastic)
      • isotropic: \(E\) = 205 \(GPa\), \(\nu\) = 0.3 and reference temperature \(T_o\) = 293.15 \(K\)

    Boundary Conditions:

    • Fixed x-translation of face ABCD and face A’B’C’D’
    • Elastic support on the faces ABCD and A’B’C’D’, with a total isotropic stiffness of \(K\) = 1000 \(N \over \ m\)
    • Fixed temperature of 303.15 \(K\) on all faces.

    Reference Solution

    The analytical solution for the unit stress is given by the following equation:

    $$σ =ΔT \times \ γ \times \ E $$

    where:

    • \(ΔT\): change in temperature = 10 \(K\)
    • \(γ\): thermal expansion coefficient = 1.2e-5 \(1 \over \ K\)
    • \(E\): Young’s modulus = 205 \(GPa\)

    As a result, the analytical calculation gives a unit stress of: $$σ =24.6\ MPa $$

    Result Comparison

    Comparison of the unit stress \(\sigma\) obtained from SimScale against the reference results obtained from [Roark]\(^1\) is given in the following table:

    Case[Roark]
    \([MPa]\)    		SimScale
    \([MPa]\)    		Error
    \([\%]\)
    A24.624.60.00
    B24.624.60.00
    Table 2: Comparison of unit stress \(\sigma\) between SimScale simulation and [Roark]\(^1\)

    As shown in Table 2, the SimScale results perfectly match the analytical ones with 0.00% error.

    References

    Last updated: July 21st, 2021

    Contents