Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationValidation CasesValidation Case: Thermal Bridge Case 4 – Iron Bar

    Validation Case: Thermal Bridge Case 4 – Iron Bar

    This thermal bridge validation case belongs to heat transfer. The aim of this test case is to validate the following parameters:

    • Temperature distribution
    • Heat flow

    The simulation results of SimScale were compared to the results presented in EN ISO 10211 Standard, case 4.

    View Project

    Geometry

    The 3D geometry for this project is a thermal bridge consisting of an iron bar penetrating an insulation layer, as seen in Figure 1:

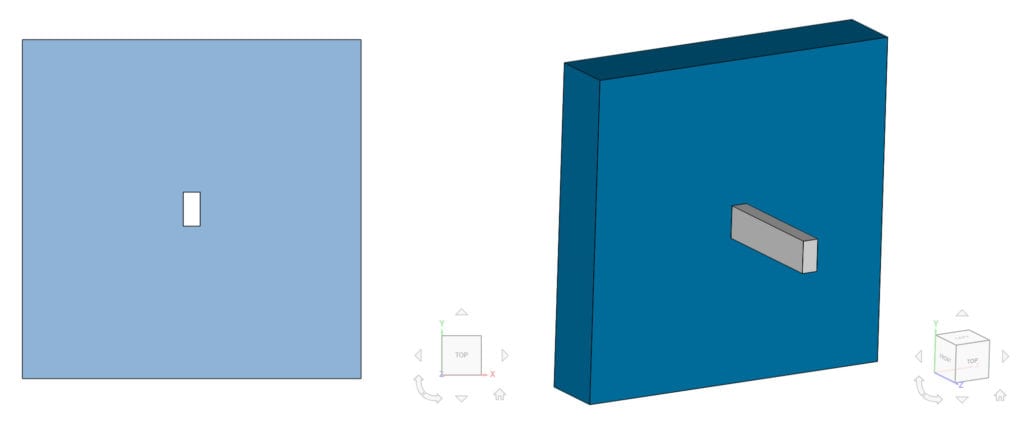
    thermal bridge geometry iso 10211 case 4 validation front and isometric view
    Figure 1: Side and isometric view of the thermal bridge geometry of an iron bar from EN ISO 10211 case 4

    The insulated wall consists of a block with a rectangular cross-section of 1×1 \(m\) and a width of 0.2 \(m\). The bar is placed vertically in the center of the wall and goes through the whole layer. It has a rectangular cross-section of 0.1×0.05 \(m\) and a total length of 0.6 \(m\), including its penetrated part.

    Analysis Type and Mesh

    Tool Type: Code_Aster

    Analysis Type: Linear, steady-state heat transfer analysis

    Mesh and Element Types: For this case, SimScale’s standard meshing algorithm was used, which generates a combination of tetrahedral and hexahedral cells. The characteristics of the resulting mesh can be seen below:

    CaseMesh TypeNodesCellsElement Type
    EN ISO 10211 Case 4Second-order standard769105553835Standard
    Table 2: Mesh details for this validation case

    In the image below, it’s possible to see the standard mesh in detail:

    standard mesher used for meshing the thermal bridge case
    Figure 2: The standard meshing algorithm generates a second order mesh, with a combination of tetrahedral and hexahedral elements.

    Simulation Setup

    Material:
    Each body is assigned to a different material:

    • Insulation layer
      • (\(\rho\)) Density: 2240 \(\frac{kg}{m^3}\)
      • Thermal conductivity: 0.1 \(\frac{W}{m.K}\)
      • Specific heat: 750 \(\frac{J}{kg.K}\)
    • Iron bar
      • (\(\rho\)) Density: 7870 \(\frac{kg}{m^3}\)
      • Thermal conductivity: 50 \(\frac{W}{m.K}\)
      • Specific heat: 480 \(\frac{J}{kg.K}\)

    Boundary Conditions:

    As shown in Figure, the following boundary conditions are defined:

    • Interior wall: Convective heat flux boundary condition:
      • (\(T_0\)) Reference temperature: 1 \(ºC\)
      • Heat transfer coefficient: 10 \(\frac{W}{m^2.K}\)
    • Exterior wall: Convective heat flux boundary condition:
      • (\(T_0\)) Reference temperature: 0 \(ºC\)
      • Heat transfer coefficient: 10 \(\frac{W}{m^2.K}\)
    • Side walls: Adiabatic in nature.

    Result Comparison

    The results obtained with SimScale were compared to those presented in [1]. The two criteria that must be satisfied are:

    • The difference in heat flow between the hot and cold sides should not deviate more than 1 % from the reference value of 0.540 \(W\).
    • The highest temperature measured in the exterior wall should not deviate more than 0.005 \(°C\) from the reference value of 0.805 \(°C\).

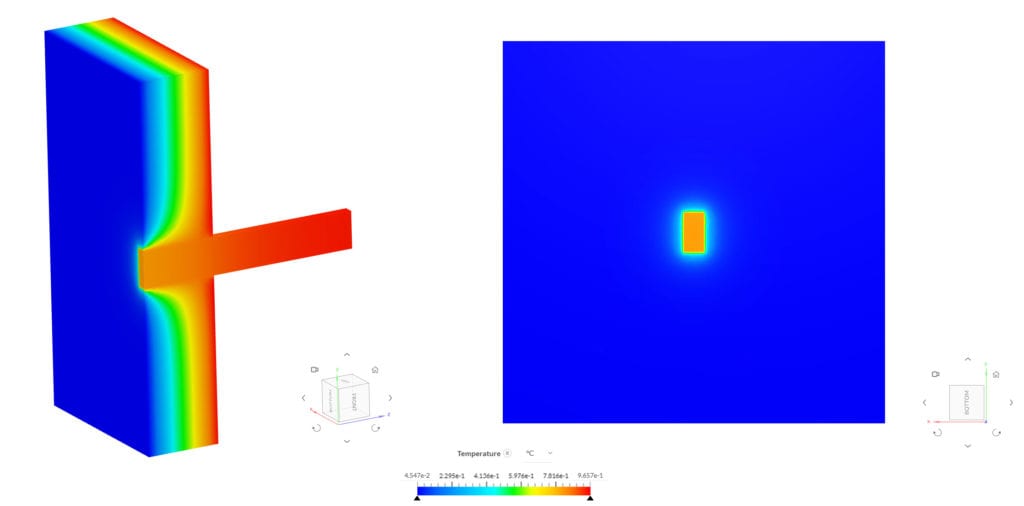
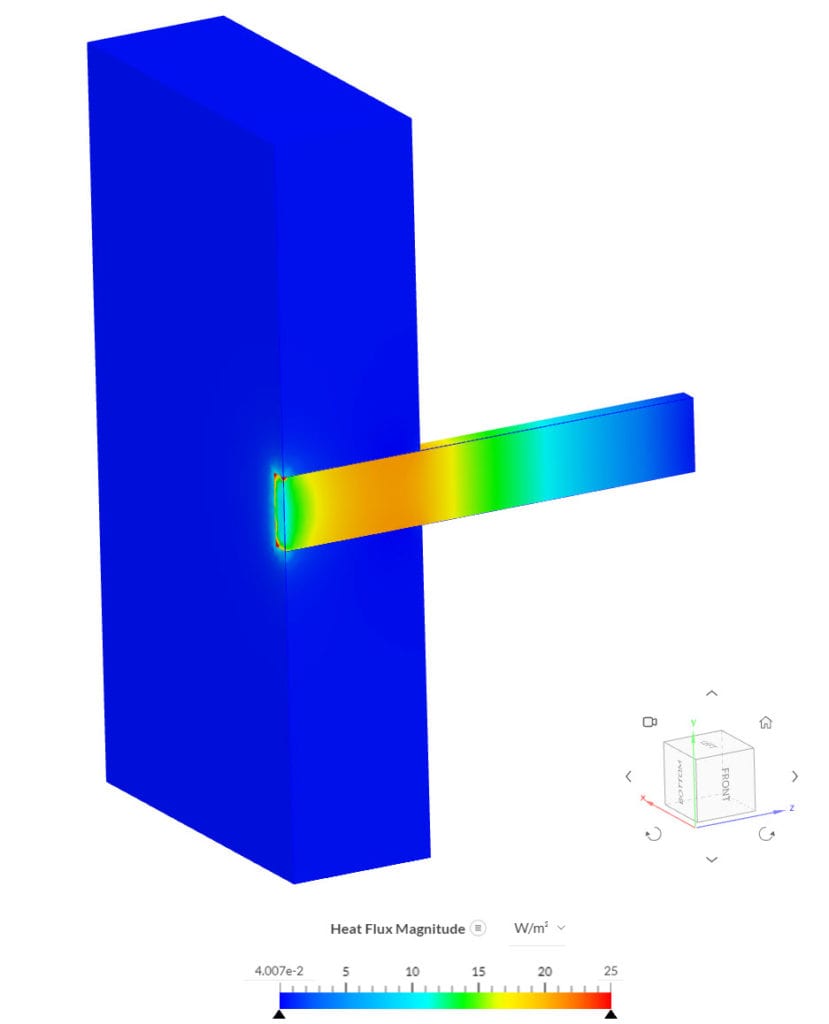
    The bulk calculator feature provided in SimScale’s integrated post-processor was used to extract the maximum temperature of the beam’s end cross-section, which is coincident with the insulation layer. The Heat Flux was measured using the Heat Flow result control Item. The table below provides an overview of the results:

    ResultReference ValueSimScale ResultDeviation
    Maximum temperature on exterior0.805\(°C\)0.803\(°C\)0.002\(°C\)
    Heat Flow0.540\(W\)0.542\(W\)-0.37%
    Table 4: Overview of the temperature results, based on the points from Figure 1

    Table 4 indicates a good agreement of the SimScale results with the reference paper, with a permitted difference between the extracted values and the standard.

    Below you can see the results of the simulation, created in the online post-processor:

    temperature distribution across thermal bridge validation case
    Figure 3: The cutting plane normal to the x-axis provides a visual representation of the temperature distribution across the beam and the insulation layer.

    Additionally, the heat flux magnitude can be visualized on the cutting plane normal to the X axis too:

    heat flux magnitude distribution across thermal bridge validation case
    Figure 4: For the calculation of the heat flow, the Heat Flux magnitude can be integrated on the end side of the beam.

    References

    Last updated: August 30th, 2022

    Contents