Fill out the form to download

Required field
Required field
Not a valid email address
Required field
Required field

  • Set up your own cloud-native simulation in minutes.

    • Documentation

    SimScale DocumentationValidation CasesValidation Case: Circular Shaft Under Torque Load

    Validation Case: Circular Shaft Under Torque Load

    This validation case belongs to solid mechanics. The aim of this test case is to validate the following parameters:

    • Torque load applied through remote force boundary condition
    • Shear stress distribution and maximum value
    • Rotational deformation magnitude

    The simulation results of SimScale were compared to the results presented in [Roark]\(^1\)

    View Project

    Geometry

    The geometry used for the case is below:

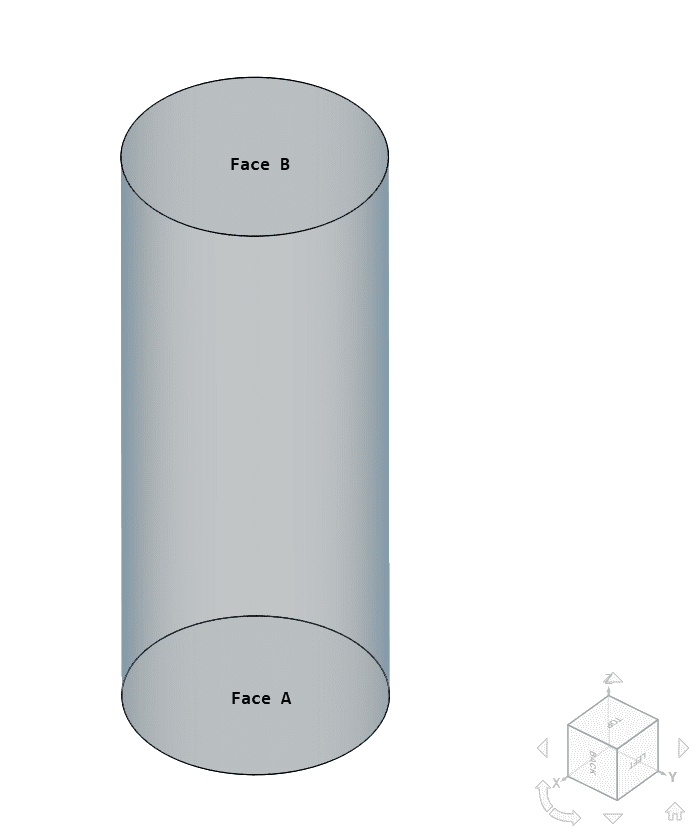
    geometrical model shaft torque load validation case
    Figure 1: Geometrical model of the shaft

    The axis of the shaft cylinder is aligned with the \(Z\) axis, with a length \(L = \) 0.5 \(m\) and a radius \(r = \) 0.1 \(m\).

    Analysis Type and Mesh

    Tool Type: Code_Aster

    Analysis Type: Linear Static

    Mesh and Element Types:

    Tetrahedral meshes were computed using SimScale’s standard meshing algorithm and manual sizing. Table 1 shows an overview of the meshes in the validation project.

    CaseMesh TypeNumber of NodesElement Type
    AStandard 1919651st order tetrahedral
    BStandard1896302nd order tetrahedral
    Table 1: Mesh details for each case

    The second order tetrahedral mesh from case B is shown in Figure 2:

    tetrahedral mesh shaft torque load validation case
    Figure 2: Shaft geometry meshes with 2nd order tetrahedral cells

    Simulation Setup

    Material:

    • Linear Elastic Isotropic:
      • \(E = \) 208 \(GPa\)
      • \(\nu = \) 0.3
      • \(G = \) 80 \(GPa \)

    Boundary Conditions:

    • Constraints:
      • Face A is fixed.
    • Loads:
      • Torque \(T = \) 50000 \(Nm\) on face B.

    Reference Solution

    The analytical solutions for the rotation angle \(\theta_B\) and maximum shear stress \(\tau_{max}\) are given by the following equations:

    \( \theta_B = \frac{ T L }{G J} \tag{1} \)

    \( \tau_{max} = \frac{T R}{J} \tag{2} \)

    \( J = \frac{\pi R^4}{2} \tag{3} \)

    The computed reference solution is:

    \( \theta_B = 1.9894×10^{-3}\ Rad \)

    \( \tau_{max} = 31.847\ MPa \)

    Result Comparison

    The plane maximum displacement \( U \) is used to compute the rotation angle through equation 4 (obtained through the cosines law):

    \( \theta = ArcCos[ 1- \frac{U^2}{2R^2} ] \tag{4} \)

    CASE\(U\)\( \theta \)\( \theta_{ref} \)ERROR
    A0.0001984630.001984630.0019894-0.24%
    B0.0001989440.001989440.00198940.00%
    Table 2: Results comparison and computed error for the rotation angle

    The maximum shear stress is taken from the Cauchy stress tensor, component [SIYZ]:

    CASESIYZ\( \tau_{ref} \)ERROR
    A31.748331.847– 0.26%
    B31.840531.847– 0.03%
    Table 3: Results comparison and computed error for shear stress

    For both 1st order and 2nd order meshes, the results show good agreement with the analytical solution. Find below an image showing the displacement magnitude on the cylinder, for case B:

    deformation color plot shaft torque load validation case
    Figure 3: Case B results, showing the displacement magnitude contours

    References

    • (2011) “Roark’s Formulas For Stress And Strain, Eighth Edition”, W. C. Young, R. G. Budynas, A. M. Sadegh.

    Note

    If you still encounter problems validating you simulation, then please post the issue on our forum or contact us.

    Last updated: July 21st, 2021

    Contents