Documentation
This validation case belongs to fluid mechanics, representing the aerodynamics of the Ahmed body study. The aim of this test case is to validate the following parameters:
The simulation results of SimScale were compared to the experimental data presented in [Ahmed]\(^1\).
The geometry is created based on the simplified aerodynamic body used by Ahmed et al\(^1\). See Figure 1 for dimensions and Figure 2 for the geometry. The slant angle (\(\phi\)) is set to 25°. The body is placed in a wind tunnel (\(6 m \times 5 m \times 13.5 m\)) in order to limit the aerodynamic blockage effect.
Tool Type: OpenFOAM®
Analysis Type: Turbulent Incompressible fluid flow
Mesh and Element Types:
| Mesh # | Mesh Type | Number of Cells | Comments |
|---|---|---|---|
| 1 | Standard | 3,826,602 | Far field mesh cell size 0.4 \(m\) |
| 2 | Standard | 4,673,973 | Far field mesh cell size 0.2 \(m\) |
| 3 | Standard | 8,594,246 | Far field mesh cell size 0.1 \(m\) |
| 4 | Standard | 10,351,196 | Body mesh cell size 3 \(mm\) |
| 5 | Standard | 24,257,180 | Body mesh cell size 2 \(mm\) |
The Standard Mesher algorithm with tetrahedral and hexahedral cells was used to generate the mesh, with refinements near the walls and in the wake region (see Figure 3).
A typical property of the generated mesh is the \(y^+\) (“y-plus“) value, which is defined as the non-dimensionalized distance to the wall, learn more. A \(y^+\) value of 1 would correspond to the upper limit of the laminar sub-layer.
Wall treatment
An average \(y^+\) value of 1 was used for the inflation layer around the body, and 150 for the floor. The \(k-\omega\) SST turbulence model was chosen, with full resolution for near-wall treatment of the flow around the body and with wall function for the floor.
Fluid
Air with a kinematic viscosity of \(1.5 \times 10^{-5}\ kg/ms\) is assigned as the domain fluid. The boundary conditions for the simulation are shown in Table 2.
Boundary Conditions
| Parameter | Inlet | Top Face | Bottom Face | Lateral Faces | Outlet | Body |
| Velocity \([m/s]\) | 60 | Symmetry | Wall Function | Symmetry | Zero Gradient | Full Resolution |
| k \([m^2/s^2]\) | 0.135 | Symmetry | Wall Function | Symmetry | Zero Gradient | Full Resolution |
| \(\omega\) \([1/s]\) | 180.1 | Symmetry | Wall Function | Symmetry | Zero Gradient | Full Resolution |
| Pressure \([Pa]\) | Zero Gradient | Symmetry | Wall Function | Symmetry | 0 | Full Resolution |
The free stream velocity of the simulation is \(60\ m/s\), so that the Reynolds number based on the length of the body \(L\) is \(4.29 \times 10^{6} \). Those are the same values presented in the original experiment of Ahmed and Ramm\(^1\).
The reference solution is of the experimental type, as presented in [Ahmed]\(^1\). It is given in terms of the drag force coefficient:
$$ C_{d} = 0.298 $$
Drag Coefficient
The drag coefficient is defined as
$$ F_{d}={\frac {1}{2}}\rho \,U^{2}\,C_{d}\,A_x $$
where \(A_x\) (0.115 \(m^2\)) is the projected area of the Ahmed body in streamwise direction and \(F_{d}\) the drag force. The time-averaged drag force was determined by integration of surface pressure and shear stress over the entire Ahmed body. The resulting drag coefficient of the Ahmed body, closest to the reference solution as yielded by the finer mesh (case number 5), was computed to be \(0.304\) which is within a \(1.94%\) error margin of the measured value.
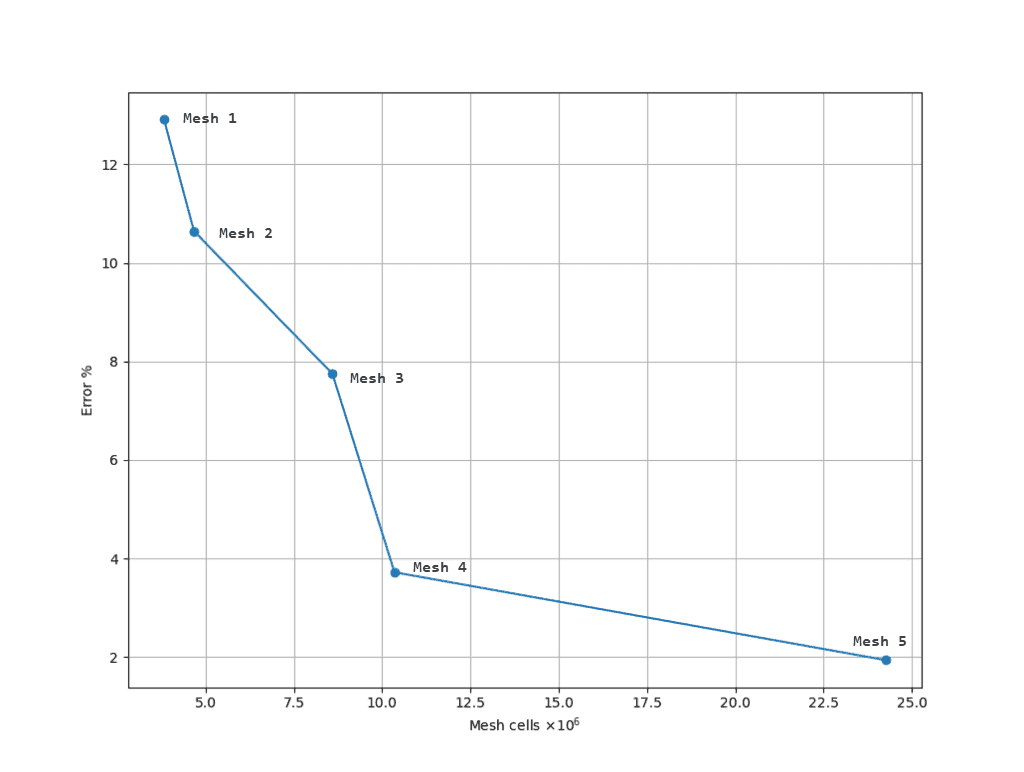
Table 3 shows the result of the mesh independence study:
| Mesh # | PRESSURE FORCE \([N]\) | VISCOUS FORCE \([N]\) | TOTAL DRAG \([N]\) | DRAG COEFFICIENT | REFERENCE | ERROR [%] |
|---|---|---|---|---|---|---|
| 1 | 76.758 | 6.540 | 83.298 | 0.336 | 0.298 | 12.91 |
| 2 | 74.992 | 6.637 | 81.629 | 0.330 | 0.298 | 10.64 |
| 3 | 72.969 | 6.524 | 79.493 | 0.321 | 0.298 | 7.75 |
| 4 | 67.671 | 8.850 | 76.521 | 0.309 | 0.298 | 3.72 |
| 5 | 64.819 | 10.387 | 75.206 | 0.304 | 0.298 | 1.94 |
Figure 4 shows the mesh convergence plot:
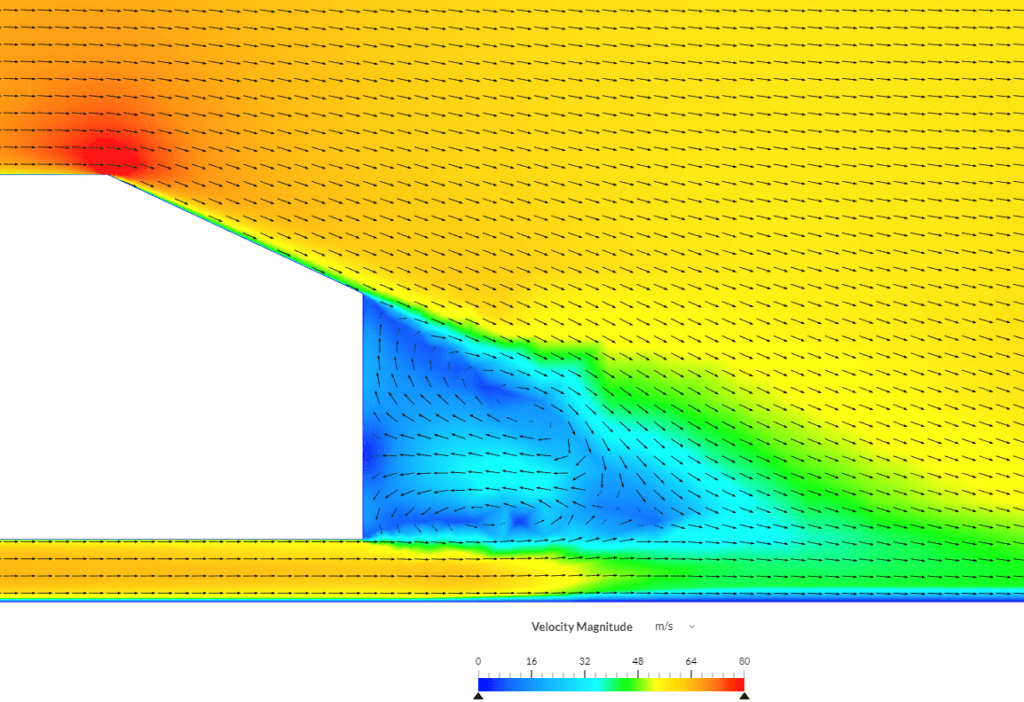
Wake Flow Patterns
The velocity streamline contour of mean flow obtained with the simulation is reported in Figure 5 together with experimental results of reference.
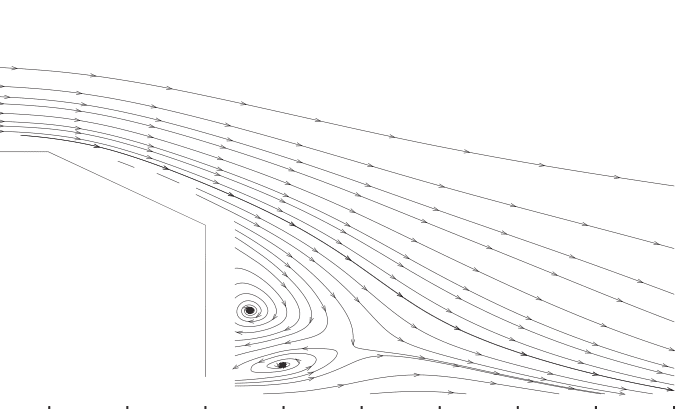
Note
If you still encounter problems validating you simulation, then please post the issue on our forum or contact us.
Last updated: December 15th, 2023
We appreciate and value your feedback.
Sign up for SimScale
and start simulating now